目录

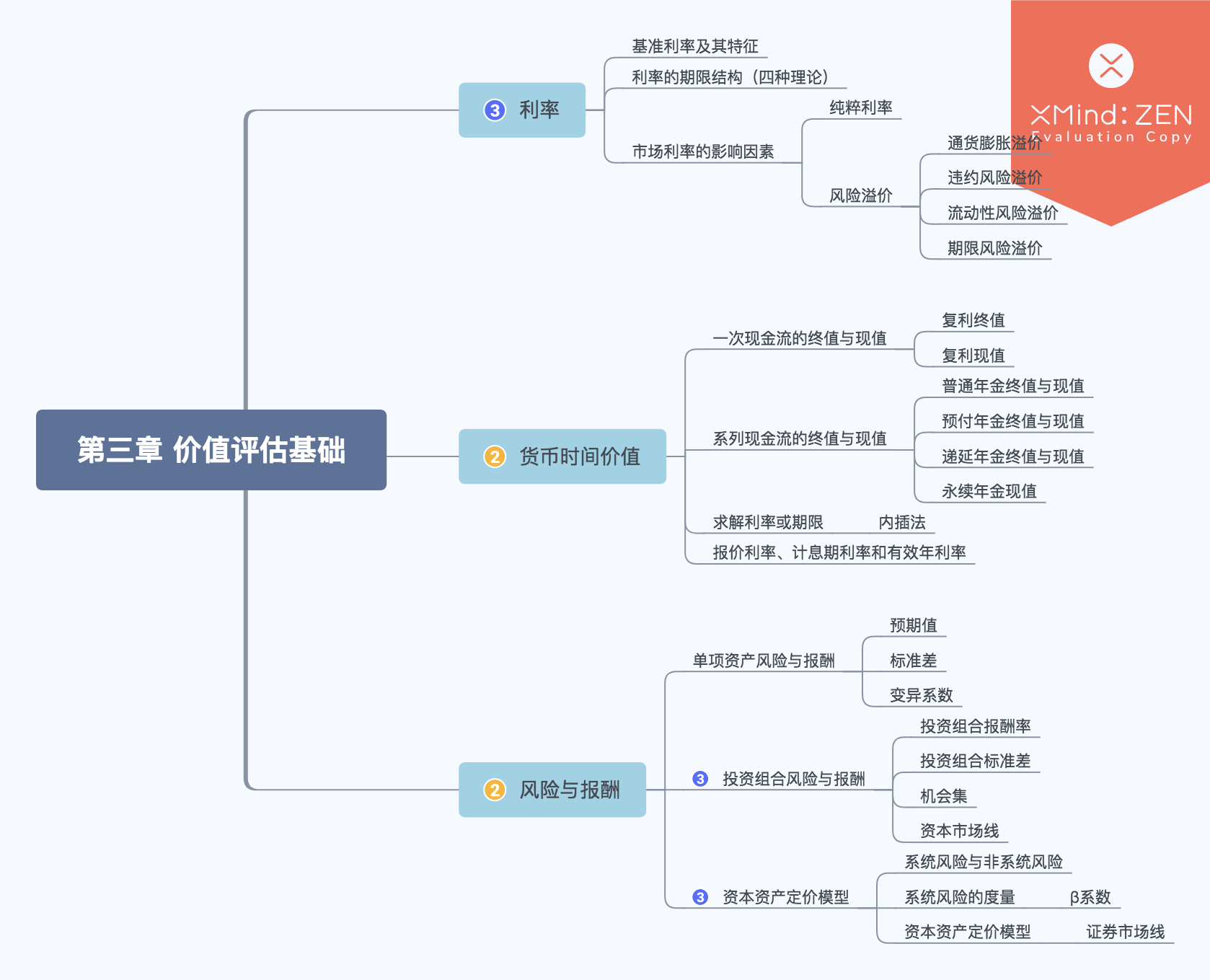
第三章 价值评估基础

利率 ★★★

市场利率的影响因素

\[ 市场利率 = 纯粹利率 + 风险溢价 \]

1. 纯粹利率---无通货膨胀、无风险情况下的市场平均利率（真实无风险利率）
2. 风险溢价
   1. 通货膨胀溢价 $ 名义无风险利率（无风险利率） = 纯粹利率 + 通货膨胀溢价$
   2. 违约风险溢价 政府违约风险溢价为零；公司评级越高，公司违约风险溢价越低
   3. 流动性风险溢价 越容易转让（国债，信誉好的公司），流动性风险溢价越低
   4. 期限风险溢价（市场利率风险溢价）期限越长，期限风险溢价越高

货币时间价值 ★★

终值与现值

1. 复利终值
   1. \(F = P \times (1 + i) ^{n}\)
   2. \(F = P \times (F/P,i,n)\)
2. 复利现值
   1. \(P = \frac{F}{(1 + i)^{n}}\)
   2. \(P = F \times (P/F,i,n)\)---复利现值系数与复利终值系数互为倒数
3. 普通年金（每期）现值
   1. \(P = A \times \frac{1-(1+i)^{-n}}{i} = A \times \frac{1-(P/F,i,n)}{i}\)---普通年金现值系数是n个复利现值系数之和
   2. \(P = A \times (P/A,i,n)\)

   

4. 投资回收额
   1. \(A = \frac{P}{(P/A,i,n)}\)---投资回收系数与普通年金现值系数互为倒数
5. 普通年金终值
   1. \(F = A \times \frac{(1+i)^{n}-1}{i} = A \times \frac{(F/P,i,n)-1}{i}\)---普通年金终值系数是n个复利终值系数之和
   2. \(F = A \times (F/A,i,n)\)

   uploading-image-617609.png

6. 偿债基金
   1. \(A = \frac{F}{(F/A,i,n)}\)---偿债基金系数与普通年金终值系数互为倒数
7. 预付年金现值
   1. \(P = A + A \times (P/A,i,n-1) = A \times [1+(P/A,i,n-1)]\)

      

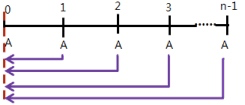
   2. \(P = A \times (P/A,i,n) \times (1+i)\)

      
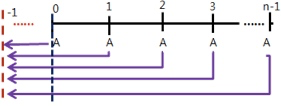
8. 预付年金终值
   1. \(F = A \times (F/A,i,n) \times (1+i)\)

      

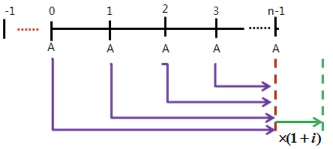
   2. \(F = A \times (F/A,i,n+1) -A = A \times [(F/A,i,n+1)-1]\)

      
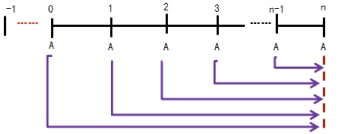
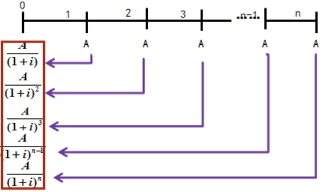
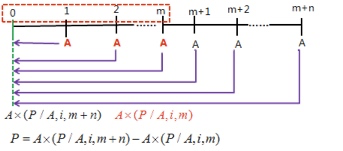
9. 递延年金现值（递延m期，m+1期后年金，合计m+n期）
   1. \(P = A \times (P/A,i,n) \times (P/F,i,m)\)

      

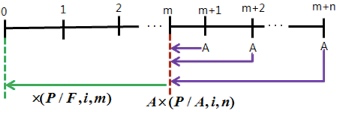
   2. \(P = A \times [(P/A,i,m+n) - (P/A,i,m)]\)

      
10. 递延年金终值（递延m期，m+1期后年金，合计m+n期）
    1. \(F = A \times (F/A,i,n)\)

    

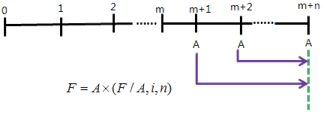
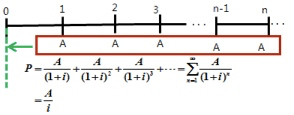
11. 永续年金现值
    1. \(P = \frac{A}{i}\)

    

报价利率、计息期利率和有效年利率

1. 报价利率
   1. 金融机构提供的利率，并提供每年复利次数
2. 计息期利率
   1. \(计息期利率 = \frac{报价利率}{每年复利次数}\)
3. 有效年利率
   1. 按照复利计算的年利率
   2. \(有效年利率 = (1 + \frac{报价利率}{每年复利次数})^{每年复利次数} - 1\)

风险与报酬 ★★

单项资产风险与报酬

1. 预期值
   1. 各个变量值出现概率已知，预期值为\(\overline{K} = \sum\limits_{i=1}^n(P_{i}K_{i})\)
   2. 各个变量值出现概率未知，预期值为\(\overline{K} = \frac{\sum\limits_{i=1}^nKi}{n}\)
2. 标准差
   1. 各个变量出现概率已知，标准差为\(\sigma = \sqrt{\sum\limits_{i=1}^n(K_{i}-\overline{K})^2 \times P_{i}}\)
   2. 各个变量出现概率未知，标准差为\(\sigma = \sqrt{\frac{\sum\limits_{i=1}^n(K_{i}-\overline{K})^2}{n-1}}\)

   n: 总体标准差

   n-1: 样本标准差

3. 变异系数
   \(变异系数 = \frac{标准差}{预期值}\)

投资组合的风险与报酬 ★★★

1. 投资组合的期望报酬率
   1. 个别报酬率的加权平均值
   2. \(R_{p} = \sum_{j}R_{j}A{j}\)
2. 投资组合的标准差
   1. \(\sigma_{p} = \sqrt{A_{1}^{2}\sigma_{1}^{2} + A_{2}^{2}\sigma_{2}^{2} + 2 A_{1}A_{2}\sigma_{1}\sigma_{2}r_{12}}\)

      \(A_{1}、A_{2}\):两种证券的投资比重

      \(\sigma_{1}、\sigma_{2}\):两种证券的标准差

      \(r_{12}\):两种证券的相关系数

   2. 相关系数
      1. \(r_{jk} = \frac{\sigma_{jk}}{\sigma_{j}\sigma_{k}}\)

      2. \(r_{jk} \in [-1,1]\)

         -1 负相关，幅度相同，方向相反

         0 不相关

         1 正相关，幅度相同，方向相同
   3. 协方差
      1. \(\sigma_{jk} = \frac{1}{n-1} \sum{(R_{j·n} - \overline{R}_{j})(R_{k·n} - \overline{R}_{k})}\)
      2. \(\sigma_{jk} = r_{jk}\sigma_{j} \sigma_{l}\)
   4. 充分投资组合的风险，只受证券之间协方差的影响，而与各证券本身的方差无关。
   5. 相关系数对两种证券投资组合标准差的影响
      1. 相关系数为1时(个别标准差加权平均值)(Max):\(\sigma_{p} = A_{1}\sigma_{1}+A_{2}\sigma_{2}\)
      2. 相关系数为-1时(Min):\(\sigma_{p} = |A_{1}\sigma_{1}-A_{2}\sigma_{2}|\)
      3. 相关系数为0时:\(\sigma_{p} = \sqrt{A_{1}^{2}\sigma_{1}^{2}+A_{2}^{2}\sigma_{2}^{2}}\)

3. 机会集

   1. 机会集曲线向左凸出，揭示了风险分散化效应。（相关系数为0的机会集曲线）
      

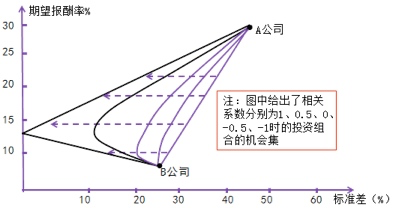
   完全正相关的投资组合（相关系数等于1），机会集是一条直线，没有风险分散化效应；

   证券报酬率之间相关系数越小，机会集曲线越弯曲，风险分散效果越强；

   部分机会集曲线没有向左凸出现象（如相关系数为0.5），即没有风险分散化效应；

   1. 有效集与无效集
   2. 多种证券组合的机会集是一个平面，但其有效集是在外围边界，并从最小方差组合点至最高报酬率点止。
4. 证券投资组合策略的选择（资本市场线的应用）
   1. 贷出资金和接入资金的证券组合策略
   2. 组合的总期望报酬率和总标准差
      1. \(总期望报酬率 = Q \times （风险组合的期望报酬率） + （1-Q）\times 无风险报酬率\)

      2. \(总标准差 = Q \times \sigma_{风险组合}\)

         \(\sigma_{无风险} = 0；\)

         Q表示投资与风险资产的投资比例；

         \(总标准差 = \sqrt{Q^2·\sigma_{风险组合}^2 + (1-Q)^2·\sigma_{无风险}^2+2·Q·(1-Q)·\sigma_{风险组合}·\sigma_{无风险}·r}\)

         如果存在贷出资金，Q小于1，投资者承担风险低于市场平均风险

         如果存在接入资金，Q大于1，投资者承担风险高于市场平均风险

      3. 资本市场线

         

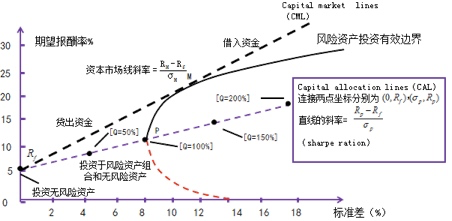
      资本市场线是通过无风险资产报酬率，向风险资产有效边界所做的切线（即同时持有无风险资产和风险资产）

      市场均衡点M是所有证券以各自总市场价值为权数的加权平均组合，是唯一有效的风险资产组合（市场组合）

      资本市场线揭示了持有不同比例无风险资产和市场组合情况下风险与期望报酬率的权衡关系，其截距是无风险报酬率，斜率代表风险的市场价格

      投资者个人风险偏好不影响最佳风险资产组合，只影响借入或贷出资金的数量

资本资产定价模型 ★★★

系统风险与非系统风险

1. 系统风险（市场风险，不可分散风险）
2. 非系统风险（公司特有风险，可分散风险）

系统风险的度量

1. 单项资产的β系数
   1. 某一资产报酬率波动与市场组合报酬率波动之间的相关性，即市场投资组合的报酬率每变动1%，期望的证券报酬率变动的百分比，是系统风险的度量指标
   2. \(\beta_{J} = r_{JM} \times \frac{\sigma_{j}}{\sigma_{M}}\)
   3. 市场组合的贝塔系数是1，无风险资产的贝塔系数是0
   4. β系数的经济意义
      1. 当β=1时，说明该单项资产的报酬率与整个市场组合平均报酬率变动幅度一致，其系统风险与整个市场组合的风险一致；
      2. 当β>1时，说明该单项资产的报酬率变动幅度大于整个市场组合平均报酬率变动幅度，其系统风险大于整个市场组合的风险；
      3. 当β<1时，说明该单项资产的报酬率变动幅度小于整个市场组合平均报酬率变动幅度，其系统风险小于整个市场组合的风险；
2. 投资组合的β系数
   1. \(\beta_p = \sum\limits_{i=1}^n{X_i · \beta_i}\)

      \(X_i各资产在投资组合中的所占比重\)
3. 资本资产定价模型
   1. \(R_i = R_f + \beta·(R_m - R_f)\)

      \(R_i\):股票的必要报酬率

      \(R_f\):无风险报酬率（国库券报酬率）

      \(R_m\):平均股票必要报酬率（市场组合必要报酬率）

      \(R_m - R_f\):风险价格（市场风险溢价）

      \(\beta·(R_m-R_f)\):股票风险溢价

   2. 证券市场线
      1. 

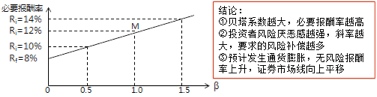
   3. 证券市场线与资本市场线比较

      比较内容	证券市场线	资本市场线
      描述的内容	市场均衡条件下（必要报酬率与期望报酬率一致）单项资产或资产组合（无论是否已经有效地分散风险）的期望收益与风险之间的关系，适合于所有证券（包括资产组合）	由风险资产和无风险资产构成的投资组合的有效边界，只适用于有效组合
      测度风险的工具	单项资产或资产组合对于整个市场组合方差的贡献程度，既β系数	整个资产组合的标准差
      斜率与投资人对待风险态度的关系	市场整体对风险的厌恶感越强，证券市场线的斜率越大，对风险资产所要求的风险补偿越大，对风险资产的要求报酬率越高	不影响直线的斜率【投资者个人对风险态度仅影响借入或贷出的资金量】

思维导图